Insolation

This notebook is part of The Climate Laboratory by Brian E. J. Rose, University at Albany.

1. Distribution of insolation¶

The amount of solar radiation incident on the top of the atmosphere (what we call the “insolation”) depends on

latitude
season
time of day

This insolation is the primary driver of the climate system. Here we will examine the geometric factors that determine insolation, focussing primarily on the daily average values.

Solar zenith angle¶

We define the solar zenith angle $\theta_s$ as the angle between the local normal to Earth’s surface and a line between a point on Earth’s surface and the sun.

From the above figure (reproduced from Hartmann (1994)), the ratio of the shadow area to the surface area is equal to the cosine of the solar zenith angle.

Instantaneous solar flux¶

We can write the solar flux per unit surface area as

Q = S_0 \left( \frac{\overline{d}}{d} \right)^2 \cos \theta_s

(1)

where $\overline{d}$ is the mean distance for which the flux density $S_0$ (i.e. the solar constant) is measured, and $d$ is the actual distance from the sun.

Question:

what factors determine $\left( \frac{\overline{d}}{d} \right)^2$ ?
under what circumstances would this ratio always equal 1?

Calculating the zenith angle¶

Just like the flux itself, the solar zenith angle depends latitude, season, and time of day.

Declination angle¶

The seasonal dependence can be expressed in terms of the declination angle of the sun: the latitude of the point on the surface of Earth directly under the sun at noon (denoted by $\delta$ ).

$\delta$ currenly varies between +23.45º at northern summer solstice (June 21) to -23.45º at northern winter solstice (Dec. 21).

Hour angle¶

The hour angle $h$ is defined as the longitude of the subsolar point relative to its position at noon.

Formula for zenith angle¶

With these definitions and some spherical geometry (see Appendix A of Hartmann’s book), we can express the solar zenith angle for any latitude $\phi$ , season, and time of day as

\cos \theta_s = \sin \phi \sin \delta + \cos\phi \cos\delta \cos h

(2)

Sunrise and sunset¶

If $\cos\theta_s < 0$ then the sun is below the horizon and the insolation is zero (i.e. it’s night time!)

Sunrise and sunset occur when the solar zenith angle is 90º and thus $\cos\theta_s=0$ . The above formula then gives

\cos h_0 = - \tan\phi \tan\delta

(3)

where $h_0$ is the hour angle at sunrise and sunset.

Polar night¶

Near the poles special conditions prevail. Latitudes poleward of 90º- $\delta$ are constantly illuminated in summer, when $\phi$ and $\delta$ are of the same sign. Right at the pole there is 6 months of perpetual daylight in which the sun moves around the compass at a constant angle $\delta$ above the horizon.

In the winter, $\phi$ and $\delta$ are of opposite sign, and latitudes poleward of 90º- $|\delta|$ are in perpetual darkness. At the poles, six months of daylight alternate with six months of daylight.

At the equator day and night are both 12 hours long throughout the year.

Daily average insolation¶

Substituting the expression for solar zenith angle into the insolation formula gives the instantaneous insolation as a function of latitude, season, and time of day:

Q = S_0 \left( \frac{\overline{d}}{d} \right)^2 \Big( \sin \phi \sin \delta + \cos\phi \cos\delta \cos h \Big)

(4)

which is valid only during daylight hours, $|h| < h_0$ , and $Q=0$ otherwise (night).

To get the daily average insolation, we integrate this expression between sunrise and sunset and divide by 24 hours (or $2\pi$ radians since we express the time of day in terms of hour angle):

\overline{Q}^{day} = \frac{1}{2\pi} \int_{-h_0}^{h_0} Q ~dh

(5)

= \frac{S_0}{2\pi} \left( \frac{\overline{d}}{d} \right)^2 \int_{-h_0}^{h_0} \Big( \sin \phi \sin \delta + \cos\phi \cos\delta \cos h \Big) ~ dh

(6)

which is easily integrated to get our formula for daily average insolation:

\overline{Q}^{day} = \frac{S_0}{\pi} \left( \frac{\overline{d}}{d} \right)^2 \Big( h_0 \sin\phi \sin\delta + \cos\phi \cos\delta \sin h_0 \Big)

(7)

where the hour angle at sunrise/sunset $h_0$ must be in radians.

The daily average zenith angle¶

It turns out that, due to optical properties of the Earth’s surface (particularly bodies of water), the surface albedo depends on the solar zenith angle. It is therefore useful to consider the average solar zenith angle during daylight hours as a function of latidude and season.

The appropriate daily average here is weighted with respect to the insolation, rather than weighted by time. The formula is

\overline{\cos\theta_s}^{day} = \frac{\int_{-h_0}^{h_0} Q \cos\theta_s~dh}{\int_{-h_0}^{h_0} Q ~dh}

(8)

Cronin (2014) also shows that the insolation-weighted value $\overline{\cos\theta_s}^{day}$ is a good choice for minimizing scattering bias under a variety of circumstances.

To calculate $\overline{\cos\theta_s}^{day}$ , we first note that the factor $S_0 \left(\frac{\overline{d}}{d}\right)^2$ cancels out of the top and bottom of the above expression, leaving

\overline{\cos\theta_s}^{Q} = \frac{\int_{-h_0}^{h_0} \cos^2 \theta_s ~dh}{\int_{-h_0}^{h_0} \cos\theta_s ~dh}

(9)

With a bit of work, we can substitute in the expression for $\cos\theta_s$ in terms of latitude $\phi$ , declination angle $\delta$ and hour angle $h$ and integrate the numerator and denominator of the above expression. I implement the resulting formulas in the Python code below

import numpy as np
import matplotlib.pyplot as plt
from numpy import sin,cos,tan,arccos,arcsin,arctan,pi,abs

lat = np.linspace(-90., 90, 500)
phi = np.deg2rad(lat)

declinations = {'21 December': -23.45,
                'Equinox': 0.,
                '21 June': 23.45}

def hour_angle_at_sunset(delta, phi):
    return np.where( abs(delta)-pi/2+abs(phi) < 0., # there is sunset/sunrise
              arccos(-tan(phi)*tan(delta)),
              # otherwise figure out if it's all night or all day
              np.where(phi*delta>0., pi, 0.) )

def insolation_weighted_coszen(delta, phi):
    h0 = hour_angle_at_sunset(delta, phi)
    denominator = h0*sin(phi)*sin(delta) + cos(phi)*cos(delta)*sin(h0)
    numerator = (h0*(2* sin(phi)**2*sin(delta)**2 + cos(phi)**2*cos(delta)**2) + 
        cos(phi)*cos(delta)*sin(h0)*(4*sin(phi)*sin(delta) + cos(phi)*cos(delta)*cos(h0)))
    return numerator / denominator / 2

for label, delta in declinations.items():
    plt.plot(lat, np.rad2deg(arccos(insolation_weighted_coszen(np.deg2rad(delta), phi))), label=label)
plt.legend()
plt.grid()
plt.title('Insolation-weighted daily average solar zenith angle as a function of latitude');
plt.ylim(30,90);
plt.xlim(-90,90);

/var/folders/dl/j7hb106d36n501mrm8j646bxpf4y1c/T/ipykernel_1048/797907564.py:14: RuntimeWarning: invalid value encountered in arccos
  arccos(-tan(phi)*tan(delta)),
/var/folders/dl/j7hb106d36n501mrm8j646bxpf4y1c/T/ipykernel_1048/797907564.py:23: RuntimeWarning: invalid value encountered in divide
  return numerator / denominator / 2

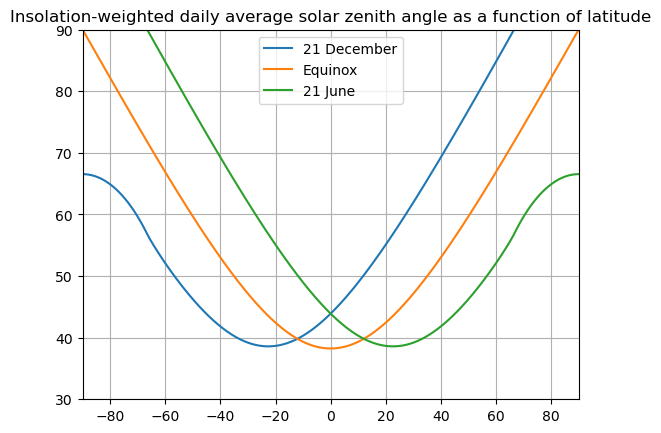
The figure above reproduces Figure 2.8 from Hartmann, 1994.

The average zenith angle is much higher at the poles than in the tropics. This contributes to the very high surface albedos observed at high latitudes.

2. Computing daily insolation with `climlab`¶

Here are some examples calculating daily average insolation at different locations and times.

These all use a function called

daily_insolation

in the package

climlab.solar.insolation

to do the calculation. The code implements the above formulas to calculates daily average insolation anywhere on Earth at any time of year.

The code takes account of orbital parameters to calculate current Sun-Earth distance.

We can look up past orbital variations to compute their effects on insolation using the package

climlab.solar.orbital

See the next lecture!

Using the `daily_insolation` function¶

from climlab import constants as const
from climlab.solar.insolation import daily_insolation

First, get a little help on using the daily_insolation function:

help(daily_insolation)

Help on function daily_insolation in module climlab.solar.insolation:

daily_insolation(
    lat,
    day,
    orb={'ecc': 0.017236, 'long_peri': 281.37, 'obliquity': 23.446},
    S0=1365.2,
    day_type=1,
    days_per_year=365.2422
)
    Compute daily average insolation given latitude, time of year and orbital parameters.

    Orbital parameters can be interpolated to any time in the last 5 Myears with
    ``climlab.solar.orbital.OrbitalTable`` (see example above).

    Longer orbital tables are available with ``climlab.solar.orbital.LongOrbitalTable``

    Inputs can be scalar, ``numpy.ndarray``, or ``xarray.DataArray``.

    The return value will be ``numpy.ndarray`` if **all** the inputs are ``numpy``.
    Otherwise ``xarray.DataArray``.

    **Function-call argument**


    :param array lat:       Latitude in degrees (-90 to 90).
    :param array day:       Indicator of time of year. See argument ``day_type``
                            for details about format.
    :param dict orb:        a dictionary with three members (as provided by
                            ``climlab.solar.orbital.OrbitalTable``)

                            * ``'ecc'`` - eccentricity

                                * unit: dimensionless
                                * default value: ``0.017236``

                            * ``'long_peri'`` - longitude of perihelion (precession angle)

                                * unit: degrees
                                * default value: ``281.37``

                            * ``'obliquity'`` - obliquity angle

                                * unit: degrees
                                * default value: ``23.446``

    :param float S0:        solar constant

                            - unit: :math:`\textrm{W}/\textrm{m}^2`

                            - default value: ``1365.2``
    :param int day_type:    Convention for specifying time of year (+/- 1,2) [optional].

                            *day_type=1* (default):
                             day input is calendar day (1-365.24), where day 1
                             is January first. The calendar is referenced to the
                             vernal equinox which always occurs at day 80.

                            *day_type=2:*
                             day input is solar longitude (0-360 degrees). Solar
                             longitude is the angle of the Earth's orbit measured from spring
                             equinox (21 March). Note that calendar days and solar longitude are
                             not linearly related because, by Kepler's Second Law, Earth's
                             angular velocity varies according to its distance from the sun.
    :raises: :exc:`ValueError`
                            if day_type is neither 1 nor 2
    :returns:               Daily average solar radiation in unit
                            :math:`\textrm{W}/\textrm{m}^2`.

                            Dimensions of output are ``(lat.size, day.size, ecc.size)``
    :rtype:                 array


    Code is fully vectorized to handle array input for all arguments.

    Orbital arguments should all have the same sizes.
    This is automatic if computed from
    :func:`~climlab.solar.orbital.OrbitalTable.lookup_parameters`

        For more information about computation of solar insolation see the
        :ref:`Tutorial` chapter.

    .. note::

        Calling ``insolation = daily_insolation(lat, day, orb, S0)`` is equivalent to::

            coszen, irradiance_factor = daily_insolation_factors(lat, day, orb)
            insolation = S0 * irradiance_factor * coszen

        Computing the zenith angle with ``daily_insolation_factors`` allows for
        optional time averaging choices which may be important for certain
        radiative transfer calculations that are sensitive to zenith angle.

Here are a few simple examples.

First, compute the daily average insolation at 45ºN on January 1:

daily_insolation(45,1)

np.float64(123.95321551807461)

Same location, July 1:

daily_insolation(45,181)

np.float64(482.356497522712)

We could give an array of values. Let’s calculate and plot insolation at all latitudes on the spring equinox = March 21 = Day 80

lat = np.linspace(-90., 90., 30)
Q = daily_insolation(lat, 80)
fig, ax = plt.subplots()
ax.plot(lat,Q)
ax.set_xlim(-90,90); ax.set_xticks([-90,-60,-30,-0,30,60,90])
ax.set_xlabel('Latitude')
ax.set_ylabel('W/m2')
ax.grid()
ax.set_title('Daily average insolation on March 21')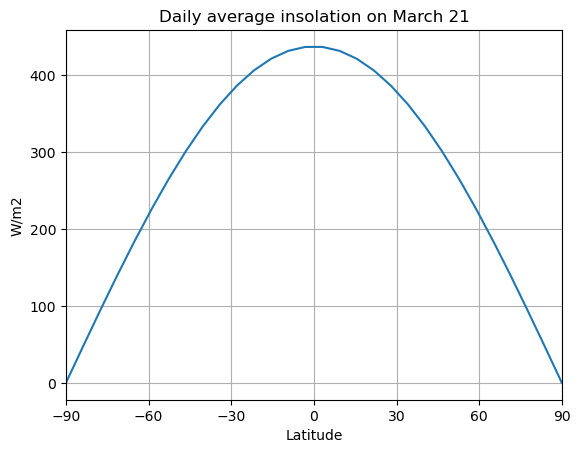

In-class exercises¶

Try to answer the following questions before reading the rest of these notes.

What is the daily insolation today here at Albany (latitude 42.65ºN)?
What is the annual mean insolation at the latitude of Albany?
At what latitude and at what time of year does the maximum daily insolation occur?
What latitude is experiencing either polar sunrise or polar sunset today?

3. Global, seasonal distribution of insolation (present-day orbital parameters)¶

Calculate an array of insolation over the year and all latitudes (for present-day orbital parameters). We’ll use a dense grid in order to make a nice contour plot

lat = np.linspace( -90., 90., 500)
numpoints = 365.
days = np.linspace(1., numpoints, 365)/numpoints * const.days_per_year

Q = daily_insolation( lat, days )

And make a contour plot of Q as function of latitude and time of year.

fig, ax = plt.subplots(figsize=(10,8))
CS = ax.contour( days, lat, Q , levels = np.arange(0., 600., 50.) )
ax.clabel(CS, CS.levels, inline=True, fmt='%1.0f', fontsize=10)
ax.set_xlabel('Days since January 1', fontsize=16 )
ax.set_ylabel('Latitude', fontsize=16 )
ax.set_title('Daily average insolation', fontsize=24 )
ax.contourf ( days, lat, Q, levels=[-1000., 0.], colors='k' )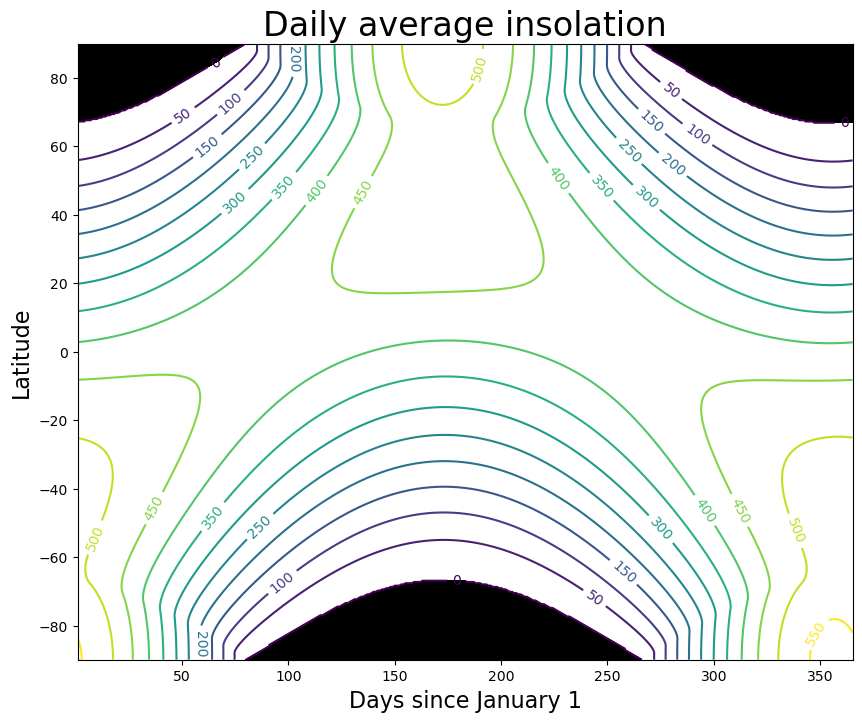

Time and space averages¶

Take the area-weighted global, annual average of Q...

Qaverage = np.average(np.mean(Q, axis=1), weights=np.cos(np.deg2rad(lat)))
print( 'The annual, global average insolation is %.2f W/m2.' %Qaverage)

The annual, global average insolation is 341.35 W/m2.

Also plot the zonally averaged insolation at a few different times of the year:

summer_solstice = 170
winter_solstice = 353
fig, ax = plt.subplots(figsize=(10,8))
ax.plot( lat, Q[:,(summer_solstice, winter_solstice)] );
ax.plot( lat, np.mean(Q, axis=1), linewidth=2 )
ax.set_xbound(-90, 90)
ax.set_xticks( range(-90,100,30) )
ax.set_xlabel('Latitude', fontsize=16 );
ax.set_ylabel('Insolation (W m$^{-2}$)', fontsize=16 );
ax.grid()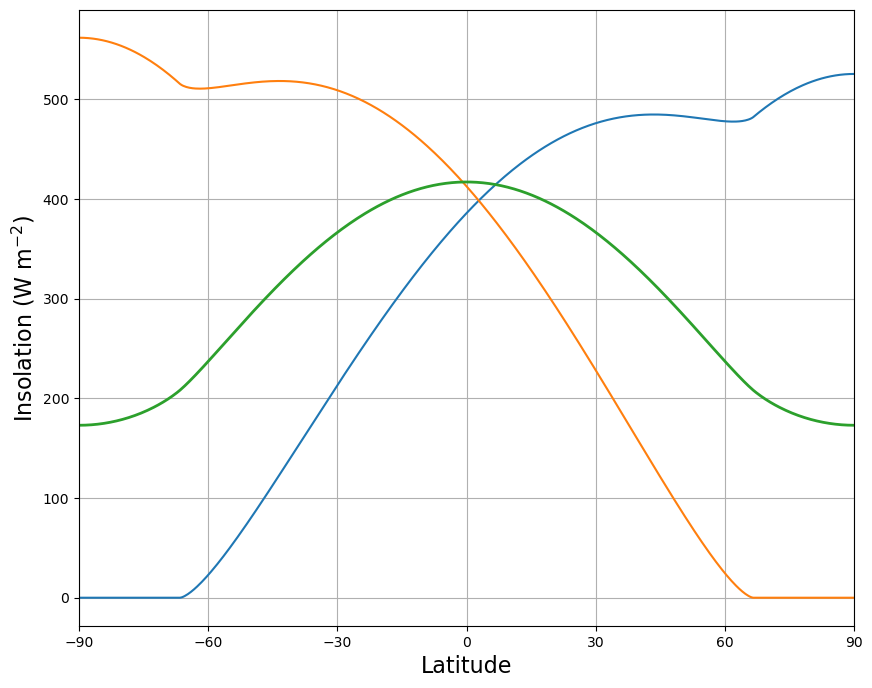

Credits¶

This notebook is part of The Climate Laboratory, an open-source textbook developed and maintained by Brian E. J. Rose, University at Albany.

It is licensed for free and open consumption under the Creative Commons Attribution 4.0 International (CC BY 4.0) license.

Development of these notes and the climlab software is partially supported by the National Science Foundation under award AGS-1455071 to Brian Rose. Any opinions, findings, conclusions or recommendations expressed here are mine and do not necessarily reflect the views of the National Science Foundation.

References¶

Hartmann, D. L. (1994). Global Physical Climatology (Vol. 56). Academic Press.
Cronin, T. W. (2014). On the Choice of Average Solar Zenith Angle. J. Atmos. Sci., 71, 2994–3003. 10.1175/JAS-D-13-0392.1

The Climate Laboratory

Clouds and cloud feedback

The Climate Laboratory

Orbital variations, insolation, and the ice ages

1. Distribution of insolation¶

Solar zenith angle¶

Instantaneous solar flux¶

Calculating the zenith angle¶

Declination angle¶

Hour angle¶

Formula for zenith angle¶

Sunrise and sunset¶

Polar night¶

Daily average insolation¶

The daily average zenith angle¶

2. Computing daily insolation with climlab¶

Using the daily_insolation function¶

In-class exercises¶

3. Global, seasonal distribution of insolation (present-day orbital parameters)¶

Time and space averages¶

Credits¶

2. Computing daily insolation with `climlab`¶

Using the `daily_insolation` function¶