Ctrl+K

Top-of-Atmosphere Radiation Budget and Meridional Energy Transport

1. Top-of-Atmosphere Radiation Budget and Meridional Energy Transport#

Overview and goals#

In this assignment you will use data from the CERES-EBAF product as we did in the first set of lecture notes.

This assigment has several goals:

  1. Build skills in loading and manipulating datasets

  2. Compute global averages

  3. Verify the data against a published result

  4. Learn the basic method for calculating meridional transport from local imbalances

  5. Apply that method to compute meridional energy transport from the CERES-EBAF data

Instructions#

  • In a local copy of this notebook add your answers in additional cells.

  • Complete both problems below.

  • Remember to set your cell types to Markdown for text, and Code for Python code!

  • Include comments in your code to explain your method as necessary.

  • Remember to actually answer the questions. Written answers are required (not just code and figures!)

  • Submit your solutions in a single Jupyter notebook that contains your text, your code, and your figures.

  • Make sure that your notebook runs cleanly without errors:

    • Save your notebook

    • From the Kernel menu, select Restart & Run All

    • Did the notebook run from start to finish without error and produce the expected output?

    • If yes, save again and submit your notebook file

    • If no, fix the errors and try again.

Problem 1: global, annual mean energy budgets#

Consider the first figure in our lecture notes from Stephens et al. [2012] and reproduced again here:

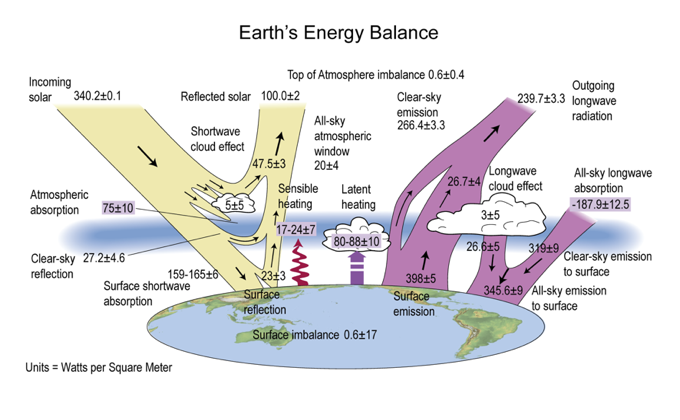
Earth's Energy Balance

Your task here is simply to reproduce as many of the values shown in this figure as you can from the CERES-EBAF dataset. Remember that these values all represent long-term time averages and global averages, and that global averages must be properly weighted to account for the area of grid cells. If you’re looking for help on the area weighting, check out this short lesson from the xarray docs.

Please include all your code here in the notebook, but also summarize your results clearly. This might be as a table, or formatted output from Python code, or any other way which is easy to read and compare against the values in the figure.

Comment on any interesting similarities or differences that you find between your results and the values in the figure.

To get you started, here is the same code we used in the lecture notes to access the CERES-EBAF data:

import xarray as xr

ceres_path = '/nfs/roselab_rit/data/CERES_EBAF/'
ceres_filename_prefix = 'CERES_EBAF_Ed4.1_Subset_'
ceres_files = [ceres_path + ceres_filename_prefix + '200003-201412.nc',
               ceres_path + ceres_filename_prefix + '201501-202202.nc',]

ceres = xr.open_mfdataset(ceres_files)
ceres

<xarray.Dataset>
Dimensions:                      (lon: 360, lat: 180, time: 264)
Coordinates:
  * lon                          (lon) float32 0.5 1.5 2.5 ... 357.5 358.5 359.5
  * lat                          (lat) float32 -89.5 -88.5 -87.5 ... 88.5 89.5
  * time                         (time) datetime64[ns] 2000-03-15 ... 2022-02-15
Data variables: (12/41)
    toa_sw_all_mon               (time, lat, lon) float32 dask.array<chunksize=(178, 180, 360), meta=np.ndarray>
    toa_lw_all_mon               (time, lat, lon) float32 dask.array<chunksize=(178, 180, 360), meta=np.ndarray>
    toa_net_all_mon              (time, lat, lon) float32 dask.array<chunksize=(178, 180, 360), meta=np.ndarray>
    toa_sw_clr_c_mon             (time, lat, lon) float32 dask.array<chunksize=(178, 180, 360), meta=np.ndarray>
    toa_lw_clr_c_mon             (time, lat, lon) float32 dask.array<chunksize=(178, 180, 360), meta=np.ndarray>
    toa_net_clr_c_mon            (time, lat, lon) float32 dask.array<chunksize=(178, 180, 360), meta=np.ndarray>
    ...                           ...
    sfc_net_tot_all_mon          (time, lat, lon) float32 dask.array<chunksize=(178, 180, 360), meta=np.ndarray>
    sfc_net_tot_clr_c_mon        (time, lat, lon) float32 dask.array<chunksize=(178, 180, 360), meta=np.ndarray>
    sfc_net_tot_clr_t_mon        (time, lat, lon) float32 dask.array<chunksize=(178, 180, 360), meta=np.ndarray>
    sfc_cre_net_sw_mon           (time, lat, lon) float32 dask.array<chunksize=(178, 180, 360), meta=np.ndarray>
    sfc_cre_net_lw_mon           (time, lat, lon) float32 dask.array<chunksize=(178, 180, 360), meta=np.ndarray>
    sfc_cre_net_tot_mon          (time, lat, lon) float32 dask.array<chunksize=(178, 180, 360), meta=np.ndarray>
Attributes:
    title:        CERES EBAF TOA and Surface Fluxes. Monthly Averages and 07/...
    institution:  NASA Langley Research Center
    Conventions:  CF-1.4
    comment:      Climatology from 07/2005 to 06/2015
    version:      Edition 4.1; Release Date June 8, 2021
    DOI:          10.5067/TERRA-AQUA/CERES/EBAF_L3B004.1
# Your answer to Problem 1 begins here!

Problem 2: Computing meridonal energy transport#

The problem#

In this problem you will tackle the problem of computing the total meridional (i.e. north-south) energy transport that is implied from the net radiation imbalance at each latitude found in the CERES-EBAF data.

An example of this was shown in this figure in our lecture notes. For this question, we will focus just on the annual mean energy transport.

A reading assignment#

The calculation involves integrating the net imbalance (ASR - OLR) in latitude starting from one pole. To understand how this works and see the specific formula for the integral, please read through sections 4 and 5 of these notes from Brian Rose’s The Climate Laboratory.

IMPORTANT: if anything in those notes is unclear, please ask! This is material I want you to understand.

The specific goal#

Your specific goal here is to produce one figure: a plot of the poleward energy transport (labeled in units of PW) implied by the CERES-EBAF data. A few notes about this:

  • You will need to take a long-term annual time average and also zonal average of the data, and carry out the integration in latitude.

  • Your figure should have just one single line plot

  • Compare this plot against the annual mean curve show in the lecture notes (linked above)

From your results, a few things to comment on:#

  • What is the energy transport at the equator?

  • Do your results show that the energy transport goes exactly to zero at both poles? If not, explain why, and whether this presents a contradiction of the method you used to compute the result.

# Your answer to Problem 2 begins here!
Contents